Lab2vZadaci primjeri.sagews

Primjer 1

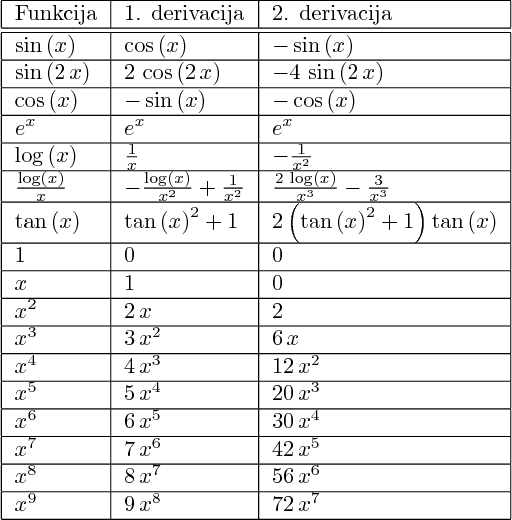
Tablica derivacija.

x=var('x')
funkcije=[sin(x),sin(2*x),cos(x),
          exp(x),ln(x),ln(x)/x,tan(x)]+\
          [x^i for i in range(10)]
show(table([['Funkcija','1. derivacija','2. derivacija']]+[[f,diff(f),diff(f,2)] for f in funkcije], frame=True, header_row=True))

Primjer 2

Sedma derivacija funkcije $$f(x) = \frac{\ln(x)}{x+1}.$$

x=var('x')
f(x)=ln(x)/(x+1)
show(f)
show(diff(f,x,7))
show(diff(f,x,7).full_simplify())

$\displaystyle x \ {\mapsto}\ \frac{\log\left(x\right)}{x + 1}$

$\displaystyle x \ {\mapsto}\ -\frac{5040 \, \log\left(x\right)}{{\left(x + 1\right)}^{8}} + \frac{720}{{\left(x + 1\right)} x^{7}} + \frac{840}{{\left(x + 1\right)}^{2} x^{6}} + \frac{1008}{{\left(x + 1\right)}^{3} x^{5}} + \frac{1260}{{\left(x + 1\right)}^{4} x^{4}} + \frac{1680}{{\left(x + 1\right)}^{5} x^{3}} + \frac{2520}{{\left(x + 1\right)}^{6} x^{2}} + \frac{5040}{{\left(x + 1\right)}^{7} x}$

$\displaystyle x \ {\mapsto}\ -\frac{12 \, {\left(420 \, x^{7} \log\left(x\right) - 1089 \, x^{7} - 2940 \, x^{6} - 4410 \, x^{5} - 4900 \, x^{4} - 3675 \, x^{3} - 1764 \, x^{2} - 490 \, x - 60\right)}}{x^{15} + 8 \, x^{14} + 28 \, x^{13} + 56 \, x^{12} + 70 \, x^{11} + 56 \, x^{10} + 28 \, x^{9} + 8 \, x^{8} + x^{7}}$

Primjer 3

Osnovne operacije na izrazima.

x,a,b=var('x,a,b')

zamjene={a:sin(x),b:cos(x)}
izraz=((a+b)^4==0)

print "Početni izraz:"
show(izraz)

print "Zamjene (python dictionary tip):"
show(zamjene)

print "Uvedimo zamjene:"
izraz=izraz.subs(zamjene)
show(izraz)

print "Izmnožimo tj. raspisujemo izraz:"
izraz=izraz.expand()
show(izraz)

print "Pojednostavimo izraz:"
izraz=izraz.full_simplify()
show(izraz)

print "Lijeva strana jednakosti:"
show(izraz.lhs())

print "Desna strana jednakosti:"
show(izraz.rhs())

print "Podijelimo originalni izraz sa 4:"
izraz=izraz/4
show(izraz)

print "Oduzmimo izrazu konstantu:"
izraz=izraz-1/4
show(izraz)

print "Dodajmo izrazu cos(x):"
izraz=izraz+cos(x)
show(izraz)

print "Kvadrirajmo izraz:"
izraz=izraz^2
show(izraz)

Primjer 4

Umnošci potencija binoma $(a+b)^n$.

a,b = var('a, b')
for i in range(15):
    show(((a+b)^i).expand())

Primjer 5

Provjera rješenja kvadratne jednadžbe - korištenje povratne vrijednosti naredbe solve. Pokušajte unijeti neku drugu jednadžbu (koju se može simbolički riješiti po $x$).

x, a, b, c = var('x,a,b,c')
jednadzbe = [a*x == b, a*x^2+b*x+c==0, sin(x)==a]

for jed in jednadzbe:
    print "Jednadžba koju rješavamo:"
    show(jed)

    print "\n\nRješenja vraćena u obliku liste:",
    view(solve(jed,x))

    print "\n\nRješenja vraćena u obliku pythonovog dictionary-a:",
    rjesenja = solve(jed,x,solution_dict=True)
    view(rjesenja)

    for rj in rjesenja:
        print "\nKoristimo rješenje: ",
        view(rj)

        jed_rj=jed.subs(rj)    # U jed se metodom subs uvrštava rješenje u obliku pythonovog dictionary-a
        print "Uvrštavamo: ", 
        view(jed_rj)

        print "Izračunavamo: ",
        jed_rj=jed_rj.expand()    # Nakon uvrštavanja rješenja izraz se prvo raspisuje
        view(jed_rj)

        print "Pokušavamo pojednostaviti naredbom 'full_simplify': ",
        jed_rj=jed_rj.full_simplify()    # Nakon raspisivanja izraz se maksimalno pojednostavljuje
        view(jed_rj)

Primjer 6

Izračunavanje limesa funkcije.

x=var('x')
expr=(2*x^3 - x -1)/(x^3 + 1)
view("$f(x) = $", expr)

lim1=limit(expr,x=+oo)
lim2=limit(expr,x=-oo)

# PAZI! - Lijevi i desni limes se ovdje razlikuju u predznaku beskonačnosti. Naredba "limit" ispisuje samo "Infinity" bez predznaka
lim4=limit(expr,x=-1)
lim4l=limit(expr,x=-1,dir='-')
lim4r=limit(expr,x=-1,dir='+')
print(lim4, lim4l, lim4r)

view('Limes od $f(x)$ kada $x$ ide u $+\infty$ je ', lim1)
view('Limes od $f(x)$ kada $x$ ide u $-\infty$ je ', lim2)
view('Limes od $f(x)$ kada $x$ ide u $-1$ je ', lim4, '  (PAZI! - limes je zapravo $\pm\infty$, tj. formalno gledano limes ne postoji.)')
view('Jednostrani lijevi limes od $f(x)$ kada $x$ ide u $-1^-$ je ', lim4l)
view('Jednostrani desni limes od $f(x)$ kada $x$ ide u $-1^+$ je ', lim4r)

expr2=exp(1/x)
view("$g(x) = $", expr2)

# PAZI! - Ovdje se lijevi i desni limes opet razlikuju. Naredba "limit" to vidi i ispisuje "und" što indicira da limes ne postoji
lim5=limit(expr2,x=0)
lim5l=limit(expr2,x=0,dir='-')
lim5r=limit(expr2,x=0,dir='+')
print(lim5, lim5l, lim5r)

view('Limes od $g(x)$ kada $x$ ide u $0$ je ', lim5, '  (Limes ne postoji.)')
view('Jednostrani lijevi limes od $g(x)$ kada $x$ ide u $0^-$ je ', lim5l)
view('Jednostrani desni limes od $g(x)$ kada $x$ ide u $0^+$ je ', lim5r)

Primjer 7

Crtanje grafa funkcije.

x=var('x')
f(x)=(2*x^3 - x -1)/(x^3 + 1)
view("$f(x) = $", f(x))
plot(f,(x,-5,5)).show(ymin=-6,ymax=6) # Crta graf funkcije f na intervalu [-5,5]. Također ograničava najveću i najmanju y-koordinatu na grafu koja se iscrtava.
#plot(f,(x,-5,5)) # Pokušajte odkomentirati i izvršiti ovu liniju, da vidite kako bi graf izgledao bez restrikcija na y-koordinatu.

# Kako ćemo naći vertikalne asimptote? U točkama gdje postoje vertikalne asimptote bi limes funkcije imao vrijednost plus ili minus beskonačno. Znači recipročna vrijednost funkcije u tim točkama bi bila jednaka 0.
show("Odredimo vertikalne asimptote rješavajući jednadžbu $1/f(x)=0$.")
show(solve(1/f(x)==0,x))
view("Od gornjih rješenja uzmimo samo jedino realno rješenje $x=-1$, a kompleksna rješenja odbacujemo. Pogledajte izračunate limese iz Primjera 6. Tamo je korištena ista funkcija $f$.")
view("Uočimo da funkcija ima vertikalnu asimptotu u -1. Nacrtajmo to malo ljepše s vertikalnom asimptotom obojanom u crveno, a kosim/horizontalnim asimptotama obojanim u zeleno.")

pol = -1     # x-koordinata vertikalne asimptote
P=plot(f,(x,-5,5))    # P će biti naš graf funkcije zajedno s označenim asimptotama. Prvo nacrtajmo sam graf funkcije.
P+=line([(pol,-10),(pol, 10)],color='red') # Nakon toga na graf dodajmo vertikalnu asimptotu.

# Računanje limesa za kose/horizontalne asimptote u punoj općenitosti
kp = limit(f(x)/x, x=+oo)
lp = limit(f(x) - kp*x, x=+oo)
km = limit(f(x)/x, x=-oo)
lm = limit(f(x) - km*x, x=-oo)
ym(x) = x*km + lm     # jednadžba pravca lijeve kose/horizontalne asimptote
yp(x) = x*kp + lp     # jednadžba pravca desne kose/horizontalne asimptote

# Dodajmo na graf još i kose/horizontalne asimptote u oba smjera
P+=plot(ym,-5,5, color='green')
P+=plot(yp,-5,5, color='green')

P.show(ymin=-6,ymax=6)    # Konačno prikažimo nacrtani graf

$f(x) =$ $\displaystyle \frac{2 \, x^{3} - x - 1}{x^{3} + 1}$

Odredimo vertikalne asimptote rješavajući jednadžbu $1/f(x)=0$.

[$\displaystyle x = \frac{1}{2} i \, \sqrt{3} \left(-1\right)^{\frac{1}{3}} - \frac{1}{2} \, \left(-1\right)^{\frac{1}{3}}$, $\displaystyle x = -\frac{1}{2} i \, \sqrt{3} \left(-1\right)^{\frac{1}{3}} - \frac{1}{2} \, \left(-1\right)^{\frac{1}{3}}$, $\displaystyle x = \left(-1\right)^{\frac{1}{3}}$]

Od gornjih rješenja uzmimo samo jedino realno rješenje $x=-1$, a kompleksna rješenja odbacujemo. Pogledajte izračunate limese iz Primjera 6. Tamo je korištena ista funkcija $f$.

Uočimo da funkcija ima vertikalnu asimptotu u -1. Nacrtajmo to malo ljepše s vertikalnom asimptotom obojanom u crveno, a kosim/horizontalnim asimptotama obojanim u zeleno.

Primjer 8.

Neka je zadana funkcija $f\colon \mathbb{R}\to\mathbb{R}$ izrazom $$f(x)=\begin{cases}ax&x<\pi/2,\\ \sin(x)& x\geq \pi/2,\end{cases}$$ u ovisnosti o realnom parametru $a$. Za koje vrijednosti parametra $a$ je funkcija $f$ neprekinuta?

x, a = var('x, a')

f1(x) = a*x
f2(x) = sin(x)

rj = solve(f1(pi/2)==f2(pi/2), a, solution_dict=True) # Uvjet neprekinutosti za x=pi/2. Tražimo rješenje za parametar a u obliku pythonovog dictionary-a
show(rj)

f1 = f1.subs(rj) # U prvu jednadžbu moramo uvrstiti pronađeno rješenje, u drugu ne moramo zato što druga jednadžba ne ovisi o parametru a
f = piecewise([[(-5,pi/2),f1],[(pi/2,10),f2]]) # Funkcija f je definirana po dijelovima preko f1 i f2
plot(f, -5, 10)

[$\displaystyle \left\{a : \frac{2}{\pi}\right\}$]